Урок математики в 6 классе
Автор: учитель математики Бондаренко Роман Петрович.
МБОУ «Каташинская СОШ» с.Сновское.
Длина окружности и площадь круга
Файл:Урок математики
Урок математики в 6 классе.
Тема: Длина окружности и площадь круга.
Цель урока
Деятельностная цель: формирование и развитие у учащихся личностных; регулятивных; познавательных и коммуникативных способов действия.
Содержательная цель: вывести формулы длины окружности и площадь круга и показать ее применение при решении задач.
Задачи:
Образовательная:
организация деятельности учащихся по применению знаний, умений и навыков при решении практических задач;
Развивающая:
развитие внимания, познавательной активности учащихся, самостоятельного применения знаний в различных ситуациях
Воспитательные:
воспитание чувства ответственности каждого школьника за собственную деятельность;
воспитание у учащихся навыков учебного труда, формирование ответственности за конечный результат, воспитание интереса к предмету
Оборудование:
компьютер, проекционное оборудование,раздаточный материал: круг с ниткой (нитка закреплена на круге)
Литература:
1) Виленкин Н.Я. Математика 6 — М.: Просвещение, 2009г;
2) Лебединцева Е.А., Беленкова Е.Ю Тетрадь по математике 5 кл – М.: Интелект-Центр, 2002г.;
Формы организации работы учащихся: фронтальная беседа, самостоятельная работа, практический эксперимент, индивидуальная.
Тип урока: урок изучения нового материала.
Форма работы: индивидуальная, работа в команде, коллективная.
Ход урока.
1.Организационный момент.
Приветствие; проверка готовности класса к уроку.
Устный счет
- Решите : (1,2-6,4)*3,4-0,8281
- Масштаб карты 1:25000. Найдите расстояние на местности, если расстояние на карте равно 4см.
- Найдите площадь квадрата со стороной 10см
- В этом ребусе зашифровано название фигуры, у которой нет ни начала, ни конца
Разгадав следующий ребус, вы узнаете, каким инструментом можно начертить самую совершенную, по мнению древних греков, плоскую фигуру.
Повторяем определение окружности: окружностью называется фигура каждая точка, которой находится на одном и том же расстоянии от центра
Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности
Диаметр (от греч. diámetros — поперечник) окружности (круга), хорда, проходящая через центр окружности.
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки окружности
Слово Круг получено из названия диаметра, что в переводе с греческого означает «Поперечник».
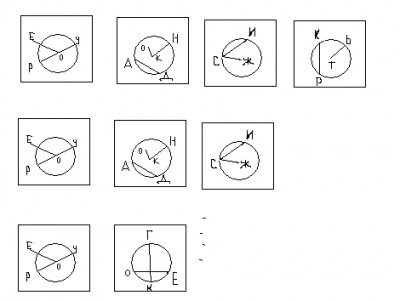
Учитель говорит понятия и поочерёдно показывает несколько карточек с изображением окружности и отрезков. Ученики пишут в тетрадях название тех отрезков, которые соответствуют понятию. Учитель говорит: «Стоп игра!», учащиеся ставят в тетради вертикальную черту. Учитель говорит следующее понятие и показывает те же карточки, ученики продолжают писать
после черты.
После выполнения упражнения, в тетрадях должна получиться запись:
ОР, ОУ, КН, СЖ, ТЬ // РУ, АД, СИ // РУ, ГК. Из полученных букв в каждой группе составить слова: окружность, радиус, круг.
Сказка: Жили – были брат и сестра. Жили они дружно, да вот беда: были они очень похожи и ребята их часто путали. Брат был солидный, плотный, а сестра тонкая и прозрачная. У брата было много друзей: диски, тарелки, монетки, блинчики. А у сестры друзей не меньше: кольца, браслеты, обручи и даже бублики… И всё у них было общее. Догадались, о чём будет идти речь на уроке?
3.Сообщение темы и цели урока.
— приведите примеры окружности и круга;
— можно ли сказать, что
срез яблока – окружность,
срез теннисного шарика – окружность,
глобус – окружность.
4.Изучение нового материала
Решение задачи «Авария на промышленном объекте»
На одном из объектов химической промышленности города АА, где в большом количестве имеются ядовитые и опасные для жизни человека вещества, произошла авария емкости с хлором. Необходимо срочно принять меры по защите населения и определения площади зараженной зоны. Известно, что в безветренную погоду хлор стелется по земле, и, распространяясь, занимает участок поверхности в форме круга
(для принятия мер класс разбит на группы и идет обсуждение проблемы – «Что предпринять?»)
В ходе обсуждения определяется круг задач:
- определить площадь зараженной территории,
- необходимость не проникновения на зараженную территорию, вычислить длину веревки для ограждения зараженной территории.
Выяснить длину веревки с помощью нитки и масштаба
из картона выполнены круги разного диаметра, к которым прикреплена нить, предназначенная для измерения длины окружности.
Длину окружности обозначают буквой С.
-Возьмите в руки круг. Что на нём отмечено? (Радиус, диаметр)
-Измерьте линейкой диаметр. Результат измерений запишите в тетрадь.
-Как вы думаете, для чего нужна нить?
-Измерьте нитью длину окружности, приложите к линейке, результат измерения запишите в тетрадь.
-Найдите отношение длины окружности к диаметру.
-Поднимите руки те, у кого число получилось больше трёх, но меньше четырёх.
Независимо от того, какого диаметра взят круг, отношение длины окружности к диаметру будет больше трёх, но меньше четырёх. Запишите в тетрадь двойное неравенство: 3 < p < 4.
| № опыта | Длина окружности (С) | Диаметр (d) | Значение С:d |
| 1 | |||
| 2 | |||
| 3 |
Если измерения выполнены достаточно точно, то у всех должно получиться значение π приблизительно равное 3,1-3,2.
| p ≈ 3,141592653589793238462643….) |
Математики договорились обозначать это число первой буквой греческого слова «Периферия» — p (пи). На некоторых кругах есть кармашек. Достаньте его содержимое и прочитайте вслух исторические сведения.
Для закрепления в памяти рационального выражения π – числа Архимеда (π =22/7)
— Первым обозначение p (пи) ввёл в1706 году английский математик Джонс.
— Французский математик Франсуа Виет нашёл значение p (пи) с девятью десятичными знаками
— В 1988 году японский учёный Ясума Канеда вычислил с помощью ЭВМ 400 миллионов цифр после запятой.
Мнемонические правила
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
- «Умная физ.минутка». Главное условие – тишина и внимание. Если вы со мной согласны, то поднимите руки вверх и опустите их вниз. Если не согласны, то выполните повороты корпуса вправо и влево. Начали!
- 3,26609 округлить до сотых. Примерно равно 3,27 (Да).
- 3,425 округлить до десятых. Примерно равно 3,3 (Нет)
- 22 = 4 (Да); 4 2 = 8 (Нет); 62 = 36 (Да)
площадь круга.
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.
6.Закрепление изученного материала
Решить №849,850, 853
7.Самостоятельная работа
I вариант II вариант
| d | C=3,14d | r | ||
| 1 | 3,14 | 254,34 | ||
| 21,98 | 11 | 379,74 | ||
| 3 | 12 | |||
| 15,7 | 907,46 | |||
| 6 | 15 |
- Итог урока. Заполнить карточку ученикам
Оцените степень сложности урока.
Вам было на уроке:
Легко 🙂
Обычно 😐
Трудно 🙁
Оцените степень вашего усвоения материала:
Усвоил полностью, могу применить;
Усвоил полностью, но затрудняюсь в применении;
Усвоил частично;
Не усвоил
Сегодня я могу оценить свою работу на «___».
- Домашнее задание по теме: «Длина окружности и площадь круга»
| 1 уровень | 2 уровень | 3 уровень |
| 1. Вычислите длину окружности и площадь круга, если
r = 5дм; 4м; 3см.
2. Найдите длину окружности, диаметр которой равен 15 дм.
3. Радиус одной окружности равен 6 см, радиус другой окружности равен 2 см. Во сколько раз первая окружность длиннее второй? |
1. Найдите диаметр окружности, если её длина равна 23,55 м. Число округлите до сотых.
2. Длина окружности круга равна 3,14 дм. Найдите площадь круга. 3. Найдите площадь круга, если длины окружности этого круга равны 24,8 см. Число округлите до десятых. 4. Останкинская телебашня в Москве имеет форму кольца. Диаметр наружной части 63 м, а внутренней окружности 44 м. Вычислите площадь фундамента телебашни. |
1. В прямоугольной пластине размерами
18 см и 41 см просверлено круглое отверстие радиусом 5 см. Найдите с точностью до 0,1 см площадь этой детали. 2. Около водопада Виктория в Центральной Африке растет баобаб, окружность ствола которого 26,2 м, а окружность ствола кипариса, растущего в Мексике, на 22,6 м больше. Определите диаметр поперечного сечения ствола баобаба и ствола кипариса. 3. Колеса автомашины Имеют диаметр 75 см. Машина едет по шоссе с такой скоростью, что каждую секунду колеса делают 8 оборотов. Найдите скорость машины. |